六、逆矩阵

       [逆矩阵及其性质] 若方阵A,B满足等式

AB=BA=I       (I为单位矩阵)

则称A为B的逆矩阵，或称B为A的逆矩阵,记作

A= 或 B=

这时A,B都称为可逆矩阵（或非奇异矩阵，或满秩矩阵）.否则称为不可逆矩阵（或奇异矩阵，或降秩矩阵）.

可逆矩阵具有性质：

1° 若A,B为可逆矩阵，则AB仍为可逆矩阵，且

（反序定律）

一般地，若A₁ ,A₂ ,…,A_s为可逆矩阵，则

       2° 矩阵A可逆的充分必要条件是：det A¹ 0.

       3° 若矩阵A可逆，则

det¹ 0 且 det=(det

=A, (a¹ 0)

=()t ,            

       4° 矩阵A可逆的充分必要条件是：矩阵A的特征值全不为零.

       [伴随矩阵与逆矩阵表达式] 设A_ij为矩阵A=(a_ij)的第i行第j列元素a_ij的代数余子式，则矩阵

A^*=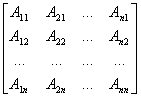

称为矩阵A的伴随矩阵.

       若A为非奇异矩阵，即det A¹ 0,则A的逆矩阵表达式为

       注意，A^*的第i行第j列元素是A的第j行第i列元素的代数余子式.

       [对角矩阵的逆矩阵] 对角矩阵

D=,   d_i¹ 0 (i=1,2,...,n)

的逆矩阵为

D^－1=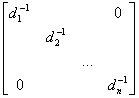

       显然对角矩阵的逆矩阵仍是对角矩阵.

       [三角形矩阵的逆矩阵] 三角形矩阵

L=,      

的逆矩阵为

=P=

式中

                     (i=1,2,...,n)

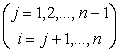
       显然非奇异下（上）三角形矩阵的逆矩阵仍是下（上）三角形矩阵.

       [正定矩阵的逆矩阵]

       1° 高斯-若当法

       正定矩阵A=(a_ij)的逆A^－1=(b_ij)可由下列递推公式求出：

,   ,      

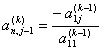                                          (k=1,2,...,n)

最后得到

式中n为该正定矩阵A的阶.

       2° 三角阵法 其步骤如下：

       （1） 把正定矩阵A=(a_ij)表示为

A=L DL t

式中D为实的非奇异对角矩阵

D=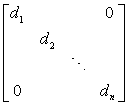

L 为实的非奇异下三角矩阵.

L =

L t 是L 的转置矩阵.d_i(i=1,2,...,n)与l_ij(i=2,...,n;j=1,…,n)由下面递推公式算出：

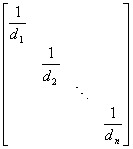
       （2）求出D的逆矩阵

=

       （3）求出L的逆矩阵

式中

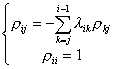
       （4）求出A的逆矩阵

=(L D=()t

=

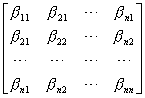
式中

       注意，这种方法的好处是避免了求平方根的运算.

       [分块矩阵的逆矩阵] 设非奇异矩阵A的分块矩阵为

A=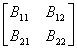

式中B₁₁,B₂₂为方子阵，那末A的逆矩阵

A^－1=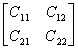

由下面公式求出

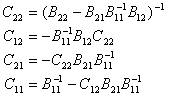
       [初等变换法求逆矩阵] 设

===B

对矩阵

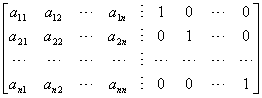
作一系列行的初等变换，使虚线左边一块矩阵化为单位矩阵，而右边一块单位矩阵就变为A的逆矩阵B=A^－1,即

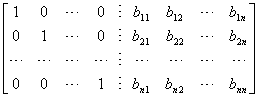
       [逆矩阵的近似求法] 设为矩阵A的初始近似逆矩阵，可由下列迭代公式求出更精确的逆矩阵：

         (n=0,1,2,...)

式中I为与A同阶的单位矩阵.

       [计算机求逆程序的检验矩阵] 用下列n阶非奇异矩阵及其逆矩阵，来检验大矩阵求逆的计算程序.

A=

=