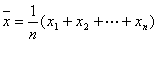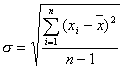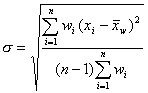二、平均值及其精密度指标
[常用平均值的求法] 设
是某观测对象的一组观测数据。
| 名称 | 定义与符号 | 用途与说明 |
| 算 术 平 均 值 | | 它在最小二乘法意义下是所求真值的最佳近似,是最常用的一种平均值 |
| 简 算 平 均 值 | 设 式中
|
|
| 几 何 平 均 值 |
| 当对一组观测值 |
| 加 权 平 均 值 | 式中 | 计算用不同方法或不同条件观测同一物理量的均值时，常对不同可靠程度的数据给予不同的“权” |
| 中 位 数 | 观测值依大小顺序排列后处在中间位置的值。当n为偶数时，取为中间两数的算术平均 | 它是一种顺序统计量，能反映匀称观测值的取值中心 |
[算术平均值与离差] 观测对象的真值x可以用n次观测值
的算术平均值.
近似代替，并用离差
代替误差
。离差与误差有如下关系
(当n相当大)
[平均值的精密度指标]
|
| 相同精密度的观测 | 不同精密度的观测 |
| 观测值 权 平均值 标准差 真值x对算术平均值 | 1 算术平均值 | 加权平均值 |
的值愈小，表明观测值的平均值
(或
)与真值x的偏差愈小，精密度愈高，即平均值可信赖的程度愈高。