§4 积分方程的近似解法
[对Fr方程的线性代数方程组的逼近法] Fr方程
（1）
可按形式
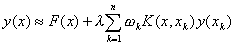
（2）
来逼近，其中xk(k=1,2,…,n)是区间[a,b]上n个适当选定的求积节点，常数ωk是对应的求积系数。如果要求在每点xk(k=1,2,…,n)处，（2）式两边相等，则得到关于n个未知函数y(x1),y(x2),…y(xn)的n个线性方程：
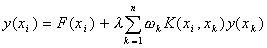
（3）
式中y(xi)(i=1,2,…n)为未知函数y(x)分别在n个点xi(i=1,2,…n)处指定的近似值。
若令
（3）可改写为
(i=1,2,…n)
写成矩阵形式为
y=F+λKWy
或 Ay=F （4）
式中A=I-λKW,I为n阶单位矩阵，K=（Kij），W为对角线矩阵
W=éw1,w 2,L,wnû ,y=(y1,y2,L,yn)t,F=(F1,F2,L,Fn)t
例 解第二类Fr方程
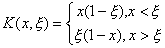
解 1° 在这个特例中，积分方程可化为具端点条件y(0)=0,y(1)=1的微分方程
其精确解为
2° 用逼近法来求近似解。取n=5个等距节点：
可以算出矩阵K 为
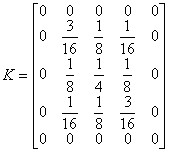
如果采用梯形法求积，那么求积系数的对角线矩阵W为
W= é
û
由于l=1，则
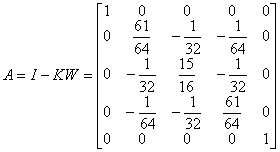
而 
解线性方程组，计算到小数点后四位得到
y1=0, y2=0.2943, y3=0.5702, y4=0.8104, y5=1
与精确解y(x)在点x=0,
和1的值
y1=0, y2=0.2940, y3=0.5697, y4=0.8100, y5=1
进行比较，可以看到误差程度。
上述方法显然可以用来求第一类Fr方程的近似解，以及处理特征值的问题。
应当指出，当核K(x,x)不是以分析表达式给定，而由实验数据确定时，上述方法特别有用。
[待定系数逼近法] 为了求积分方程
（1）
的解，可适当选择n个函数
，用它们的线性组合来逼近
其中n个系数ak（k=1，2，Ln）可以这样决定：使这个线性组合尽可能近似地满足（1），即
（a≤x≤b）
令
上式变成
（a≤x≤b） （2）
待定系数a1,a2,L,an可由n个条件决定，方法如下：
1° 配置法 令
（a≤x ≤b） （3）
为决定这n个常数a1,a2,L,an，在区间[a,b]上适当选择a≤x1<x2<L<xn≤b(xi称为配置点)，使
（i=1,2,Ln）
其矩阵形式为
ya =F (4)
式中y =(ψij)=(ψj(xi)),F=(F(x1),F(x2),LF(xn))τ为已知量，
a =（a1,a2,L,an）t
为 未 知 量。解线性方程组（4）便得到所求的系数a1,a2,L,an。
2°权函数法 设w1(x),w2(x),L,wn(x)为区间[a,b]上n个线性无关的函数（称为权函数）。为决定系数a1,a2,L,an，可以要求（3）式两边之差
与这n个权函数正交，即使得
(i=1,2,…n)
其矩阵形式为
Aa =b (5)
式中 
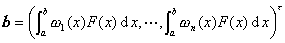
为已知量，
a =（a 1,a 2,L,a n）t
为未知量。解线性方程组（5）便得到所求的系数a 1,a 2,L,a n。
通常选取权函数w i(x)与近似函数j i(x)恒等比较方便，一般都取为
1,x,x2,L,xn-1
[核的逼近法] §1指出Fr方程的核可用x和ξ的一个多项式或一个更一般形式的可分离核来逼近，并用那里的方法来解所得的近似方程。
例 积分方程
(1)
中的核
可用多项式A1+A2x+A3x2或更适当的形式x(1-x)(B1+B2x+B3x2)来逼近，其中A,B为包含ξ的参数，采用权函数或配置点可决定A与B。
首先取一个粗糙的逼近形式
它在端点x=0和x=1是精确的，为决定系数B，可要求在[0,1]上核的积分等于它的近似表达式的积分，即
直接计算得
B=3ξ(1-ξ)
并把对应的近似核代入(1)导出近似积分方程
(2)
令
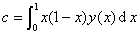
(2)式化为
y(x)=x+3cx(1-x) (3)
为了决定c，以x(1-x)乘上式的两边，并在[0,1]上积分，得
从此算出
,代入(3)得到方程(1)的近似解
更一般地，如果取近似核为
则类似地可得方程(1)的近似解
）