七、特征值与特征矢量
[特征值与特征矢量] 对n阶方阵
A=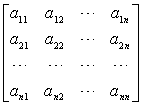
和n维非零列矢量
=(a1,a2,...,an)t
如果有一个数λ，使得
Aα=λα
则称λ为矩阵A的特征值（特征根），α为矩阵A的特征值λ所对应的特征矢量.
矩阵A的所有特征值中绝对值最大的一个称为A的第一特征值.
[特征矩阵·特征多项式· 特征方程] n阶方阵
A=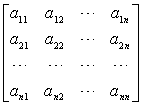
的特征矩阵定义为
式中I为n阶单位矩阵.行列式|A－λI|称为矩阵A的特征多项式，记作
j（l）=|
λI|
方程
j（l）＝０
称为矩阵A的特征方程.
[矩阵的迹与谱] n阶方阵A的主对角线上各元素之和称为A的迹，记作
特征方程j（l ）＝０的n个根l 1，l2，...，l n就是矩阵A的n个特征值.集合{l 1，l2，...，l n }称为矩阵A的谱，记作chA.
线性齐次方程组
的非零解a便是矩阵A的特征值l i所对应的特征矢量.
[特征值与特征矢量的性质]
1° 设l1，l 2，...，ln为n阶方阵A的n个特征值，则
Ak的特征值为
（k为正整数）.
A的逆矩阵A－1的特征值为
.
A的伴随矩阵A*的特征值为
.
2° n阶方阵A的n个特征值之和等于A的迹，矩阵A的n个特征值之积等于A的行列式，即
l1+l2+...+ln=a11+a22+...+ann
由此可以推出矩阵可逆的另一充分必要条件是：A的所有特征值都不为零.
3° 若li是特征方程的k重根，则对应于li的线性无关的特征矢量的个数不大于k.当li为单根时，对应于li的线性无关特征矢量只有一个.
4° 矩阵A的不同特征值所对应的特征矢量线性无关.
若n阶方阵A对应于特征值l1，l2，...，ls的线性无关的特征矢量分别有k1,k2,...,ks个，则这
个特征矢量线性无关，且
.
5° 实对称矩阵的特征值都是实数，并且有 n个线性无关（而且是正交）的特征矢量.
6° 矩阵的特征值在相似变换下保持不变，特别，At 与A具有相同的特征值.
[求第一特征值的迭代法] 在实际问题中，往往不要求算出矩阵A的全部特征值，只需算出第一特征值，用迭代法计算如下：
假定当
时，可以认为a(k) ≈a(m+1)，那末迭代到
即可.这时
为矩阵A的第一特征值的近似值，a(m+1)为所对应的特征矢量.
[求实对称矩阵的雅可比法] 设n阶实对称矩阵A=(aij)的特征值是l1，l2，...，ln，则必存在一正交矩阵Q，使得
Qt AQ=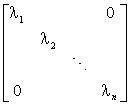
为对角矩阵.正交矩阵Q可用一系列旋转矩阵的积来逼近：
Q=
式中
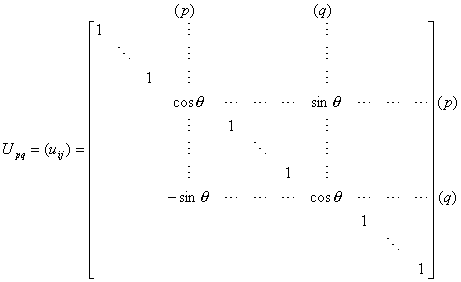
取
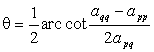
因为在这种旋转变换下，消去了矩阵中位于第p行第q列(p¹ q)交点上的元素（见本节，五），而矩阵所有元素的平方和保持不变，而且对角线上的元素的平方和增大，因而非对角线元素的平方和随之减小，因此，当旋转次数足够大时,可使非对角线元素的绝对值足够小.对于预先给定的精度e >0,如果｜aij｜<e (i¹ j),则可认为aij≈0.于是得到求矩阵A的特征值与特征矢量的具体迭代方法.
1° 按以下递推公式求特征值l1，l2，...，ln：
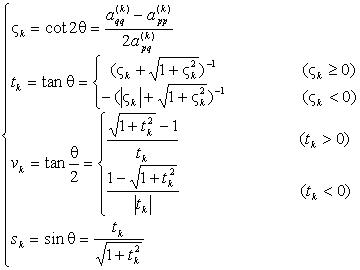
假定当
时，可以认为
，则迭代到
即可.而取
作为li的近似值：
2° 求特征矢量从1°有
=
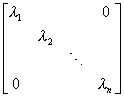
记
Pm=U1…Um-1Um
则
APm= Pm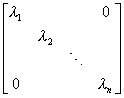
所以Pm为特征矢量矩阵.
Pm由下列递推公式算出：
最后得到 
即 
为对应于特征值l i的特征矢量的近似值.
[求对称三对角矩阵特征值的方法]
1° 相似变换法 设A为n阶对称三对角矩阵：
A=
(1)
经过相似变换
式中I为单位矩阵,tk为适当选定的常数，Ui为雅可比旋转矩阵：
为Ui的转置矩阵.又A1=A，Ak+1与
I相似，且Am与
相似.因此，若Am的特征值为
，则A1的特征值l i(i=1,2,...,n)为
(i=1,2,…,n)
假定当
时，可认为
，那末可适当选择si，ci，使得当m充分大时，Am在该精度下化为对角线矩阵；其特征值
.
(i=1,2,...,n)可由下列递推公式算出：
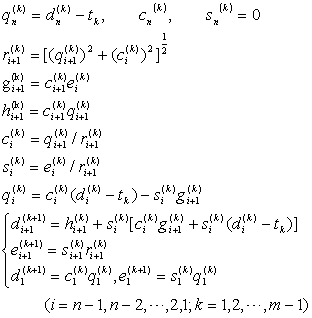
tk的选择对收敛速度影响较大，取tk为二阶矩阵
的接近于
的那个特征值，即
tk =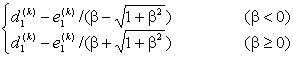
式中 
2° 二分法 设A为n阶对称三对角矩阵（如（1）式），对任意l ，设序列
q1(l )=d1?l
qi(l )=
中qi(l )<0的个数为N(l )(在这些关系式中，对于某些i，如果qi-1(l )=0，则只需用适当小的数代替即可），则N(l )等于矩阵A 的小于l 的特征值的个数.
假定矩阵A的第k个特征值lk(l1≤l2≤… ≤lk≤…≤ln) 在区间[u,
]中，令
,当N(r1)≥k时，则lkÎ [u, r1]；当N(r1)<k时，则lkÎ [ r1,];…依此类推，m步之后，l k包含在宽度为
的区间中.m充分大时，便可得到所求的特征值.