七、抛物线法（穆勒法）

求实系数n次方程

f(x)=xⁿ+a₁x^n-1+L+a_n=0              (1)

的近似根.

       可先求出f(x)=0的一个根x=r，则

                     f(x)=(x-r)g(x)

                        =(x－r)(x^n－1+b₁x^n－2+L+b_n－1)

式中g(x)是n－1次多项式，然后再求出g(x)的根，依此类推，可以求出f(x)=0的全部实根来.

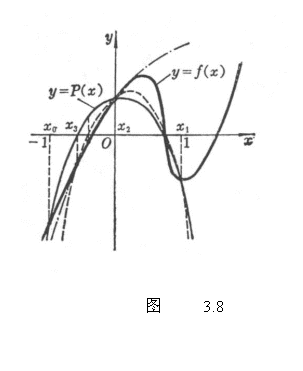
       首先选取x轴上三点：x₀,x₁,x₂,通过曲线y=f(x)上的三点：(x₀,f(x₀)), (x₁,f(x₁)),(x₂,f(x₂))作一抛物线y=P(x)（即拉格朗日插值多项式，见第十七章，§2，三），抛物线与x轴有两个交点，取离x₂较近的一点作为x₃；再过三点(x₁,f(x₁)),(x₂,f(x₂)), (x₃,f(x₃))作一抛物线（图3.8中的虚线），它与x轴有两个交点，取离x₃较近的一点作为x₄L，依此法作出点x_i-2, x_i-1,x_i，再过三点(x_i-2,f(x_i-2)),(x_i-1,f(x_i-1)),(x_i,f(x_i))作一抛物线与x轴有两个交点，取离x_i较近的一点作为x_i+1，等等.

       对于预先给定的允许误差e，当迭代过程进行到

ïx_i+1-x_iï<e

时，就取x_i+1作为f(x)=0的一个近似根.

       由此得到的序列是收敛的.极限值，就是方程f(x)=0的根.

       迭代步骤如下：

（1）根据经验对上式（1）可取

x₀=－1,  x₁=1,      x₂=0

作为初始值，于是

f(x₀)=(－1)ⁿ+(－1)^n－1a₁+L－a_n－1+a_n

f(x₁)=1+a₁+L+a_n

f(x₂)=a_n

或用x=0附近的近似值

f(x₀)»a_n－2－a_n－1+a_n

f(x₁)»a_n－2+a_n－1+a_n

f(x₂)=a_n

（2）设

                                                        l_i=,     d_i=1+l_i=

                                                        g_i=f(x_i－2)l_i² －f(x_i-1)l_id_i +f(x_i)l_i

                                                        h_i=f(x_i-2)l_i² -f(x_i-1)d_i² +f(x_i)(l_i+d_i)                       

由此根据x_i-2, x_i-1, x_i 计算出l_i, d_i, g_i, h_i，并根据下列公式计算出l_i+1

l_i+1=

       （h_i>0，根式取正号；h_i<0，根式取负号）

       当f(x_i-2)=f(x_i-1)=f(x_i)时，取l_i+1=1.

（3）根据公式

x_i+1=l_i+1(x_i－x_i-1)+x_i

计算出x_i+1