§3 随机过程
一、一、一般随机过程
[随机过程的定义] 对于每个tÎT(T 是某个固定的实数集),x (t)是个随机变量,就把这样的随机变量族{x (t),tÎT}称为随机过程。随机过程一次实验的结果是定义在T上的函数,称为随机过程的一次实现。当参数t的变化范围T是个整数集合,则称
x (t), t=0,±1,±2,L
为随机序列。
当T只包含一个或有限个元素,{x (t),tÎT}就是概率论中研究过的随机变量或随机矢量。
[随机过程的有穷维分布函数族] 设{x (t),tÎT}是随机过程,对任意的正整数n及任意的t1, t2, L,tnÎT,随机变量x (t1) ,x (t2) ,L,x (tn)的联合分布函数为
![]()
称![]() 为随机过程的有穷维分布函数族。它不仅刻划了对应于每一个t的随机变量x(t)的统计规律性,而且也刻划了各个随机变量x(t)之间的关系,从而完整地描述了随机过程的统计规律性。
为随机过程的有穷维分布函数族。它不仅刻划了对应于每一个t的随机变量x(t)的统计规律性,而且也刻划了各个随机变量x(t)之间的关系,从而完整地描述了随机过程的统计规律性。
[随机过程的统计参数] 设{x (t),tÎT}是个复值随机过程(指它的实部和虚部都是实的随机过程)。主要的统计参数有:
1° 均值函数 对每个tÎT,随机变量x(t)的数学期望(均值)
![]()
称为随机过程的均值函数,式中Ft(x)是x(t)的分布函数。
2° 协方差函数与方差函数 对任意的s, tÎT,
![]()
称为随机过程的协方差函数(或相关函数),式中m(t)是均值函数。
特别地,当s=t,则称
![]()
为随机过程的方差函数(或自相关函数)。
3° 高阶矩 若对任意的正整数n,非负整数m1 , m2,L , mn , m= m1+m2+L+mn及任意实数t1,t2,L,tn,随机变量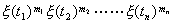 的数学期望存在,则
的数学期望存在,则

称它为x (t)在t1,t2,L,t n矩的一个m阶矩。
[随机过程的均方连续性] 设{x (t),tÎT}是一随机过程,t0ÎT,如果
![]()
即 ![]()
则称x (t)在t=t0是均方连续的,式中l.i.m.表示均方收敛。如果x(t)对于任意tÎT都是均方连续,就称x (t)在T上是均方连续的。
随机过程{x (t),tÎT}的如下三命题是等价的:
1° 随机过程{x (t),tÎT}在T上均方连续;
2° 随机过程{x (t),tÎT}的协方差函数R(s,t)(s,tÎT)关于s,t是连续的;
3° 随机过程{x (t),tÎT}的协方差函数R(s,t)(s,tÎT)在对角线s=t上关于s,t是连续的。
下面介绍几种特殊类型的随机过程:
[独立随机过程] 若对任意的正整数n和任意的t1,t2,LtnÎT,随机变量x(t1),x(t2),L,x (tn)是相互独立的,即
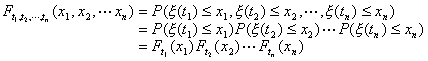
则称{x (t),tÎT}是独立随机过程。
[正态过程] 若对任意的正整数n和任意的t1,t2,L,tnÎT,随机变量x (t1),x (t2),L,x (tn)的联合分布总是正态的,即
![]()
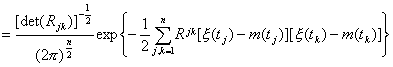
则称{x (t),tÎT}是正态(或高斯)过程,式中Rjk=R(j,k),(Rjk)称为协方差矩阵;(Rjk)是(Rjk)的逆矩阵。
[马尔科夫过程] 若对任意的n=1,2,L和任意的t0,t1,L,tnÎT(其中t0<t1<L<tn)以及任意的实数x, y,等式
P{x (tn)≤y|x (tn-1)=x,x (tn-2)=xn-2,L,x (t0)=x0}=P{x (tn)≤y|x (tn-1)=x}
对所有的x (tn-1),L, x (t0)成立,则称{x (t),tÎT}是马尔科夫过程,简称马氏过程。
[时齐马尔科夫过程] 设{x (t),tÎT}是马尔科夫过程,若对任意的t1ÎT,t2ÎT
(t1<t2),条件分布
![]()
即条件分布F(t1,x;t2,y)只依赖于t2-t1,x,y,则称{x (t),tÎT}是一个时齐(对时间齐次地)的马尔科夫过程。
[具有独立增量的随机过程] 若对 及任意一组
及任意一组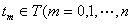 ,其中
,其中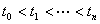 ),随机变量
),随机变量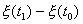 ,
, ,¼,
,¼,![]() 是相互独立的,则称
是相互独立的,则称![]() 是个具有独立增量的随机过程。
是个具有独立增量的随机过程。
[具有平稳增量的随机过程] 若对任意的t1,t2ÎT和任意h(t1+h,t2+hÎT),随机变量
x (t2+h)![]() (t1+h)与x(t2)
(t1+h)与x(t2)![]() (t1)
(t1)
遵从相同的概率分布,则称![]() 是具有平稳增量的随机过程。
是具有平稳增量的随机过程。
[泊松过程] 设{x (t),0≤t<∞}是具有平稳独立增量,取非负整数值的随机过程。如果对于任意t (0≤t<∞),关系式
![]() (k=0,1,2,L)
(k=0,1,2,L)
成立(其中λ>0为常数),则称{x (t),0≤t<∞}为泊松过程。
[维纳过程] 若随机过程{x (t),0≤t<∞}满足P(x (0)=0)=1,具有平稳独立增量,并且随机变量x (t)的分布密度函数是
![]()
则称{x (t),0≤t<∞}是维纳过程或布郎运动过程。
[平稳过程] 若对于n=1,2,L,任意tmÎT(m=1,2,L,n)及任意的τ(tm+τÎT,m=1,2,L,n),等式
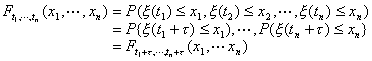
成立,则称{x (t),tÎT}是平稳过程(狭义的平稳过程)。