三、  三、        一维的弹性问题

本段只讨论柱体的扭转问题，因为它是用扭转率作为广义应变的.其他问题如杆的伸缩、梁的弯曲等可看作二维问题的简化而且与有限元法关系不大,从略.

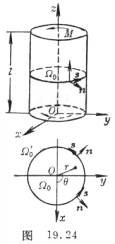[圆柱的扭转]  圆柱的半径为R,圆柱的中心轴取作z轴,两端为z=0,z=l,体力不计.首先考虑只在两端截面受相反的力偶矩M(图19.24)而产生的扭转变形.一般可假定只有沿各横截面产生抗扭的剪应力而其余的分量

       (i=1,2,3)

从物理方程可知它也是一种纯剪切变形。在圆截面上取极坐标也构成右手坐标系(图19.24)   对圆柱的扭转，还进一步假定

（i)             （i)         ，即各圆截面无轴向位移；

（ii)            （ii)       任一圆截面将绕圆心作微小的转动。

设转动角为ω(z),则ω(z)-ω(0)表示相对于端面z截面z=0的扭转角，而ω(l)-ω(0)就是柱体的总扭转角。一般可令ω(0)=0，即一端固定。

考虑半径为r在z与z+dz截面之间的环面,不难看出,由于相对扭转角dω而产生的直角改变量即剪应变

它是由环面上沿q 方向（或垂直于半径r）的剪应力作用的结果，依虎克定律

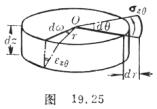
根据剪应力的对称性可得沿z截面的扭矩

式中就是截面对中心轴的惯矩。于是变形能可写成

因此，圆柱扭转问题的扭矩与扭转率可分别看作广义的剪应力与剪应变。系数称为柱体的抗扭刚度。对这问题，§1中B是微分算子，D是_，待定函数就是广义的位移即扭转角ω(z)。

推广到一般情况。如果沿柱体每单位长度施加分布荷载即扭转，则平衡方程可写成

而其边界条件同样有三种支承形式：

（i)             （i)         几何约束   对柱端截面给定扭转角ω。例如

（ii)            （ii)       荷载支承   对柱端截面施加一定的扭转。例如

或

（iii)          （iii)      弹性支承  在柱端截面给定与扭角偏差成正比的弹性反矩。例如

或

式中为弹性耦合系数。

总势能的表达式       由于体力不计，对弹性支承的情况，变形能与外力势能可分别表示ω(z)的泛函形式：

若某端为荷载支承，可取该端，则表达式照旧；若某端（例如z=0）给定扭转角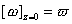，则在上二式中含端点z=0的项都要去掉，而总势能的表达式可写成

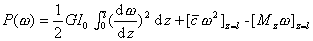
[柱体的扭转]   同圆柱扭转一样，假定，体力与侧面的面力不计，只在两端施加力偶矩M，其扭矩的位移分量可写成

其中为扭转率，称为翘曲函数。

几何方程      

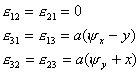
物理方程

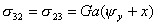
平衡方程     从可得

其中为柱体截面。

边界条件   设的边界的外法线的方向余弦为，由于柱侧面不受面力，从物理方程可得边界条件

根据，从平衡方程与边界条件可知其一般解的形式为（为任意常数）。a可由两端截面的力矩平衡条件来确定，例如从端面z=l的扭矩

可得出扭转率

于是，可看作位移，问题归结为求使总势能

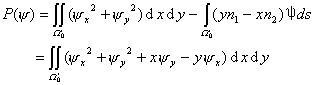
达到极值的解。