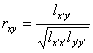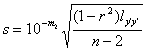2、一元线性回归
[一元回归方程] 自变量x与变量y对应的观测值为
|
|
|
|
|
|
|
|
|
|
|
|
如果变量间存在着线性关系,则可用直线
![]()
来拟合它们之间的变化关系。由最小二乘法,a,b应使
![]() 最小值
最小值
得
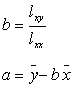
式中
![]()
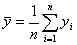
![]()
![]()
方程![]() 称为回归方程(或回归直线),b称为回归系数。
称为回归方程(或回归直线),b称为回归系数。
[相关系数及其检验表] 相关系数rxy反映了变量x和y之间的线性关系的密切程度,它是用下式定义
 其中
其中![]()
(在不致误会时,rx y简记为r)。显然![]() 。当
。当![]() 时,称为完全线性相关;当
时,称为完全线性相关;当![]() 时,称全无线性相关;当
时,称全无线性相关;当![]() 越接近1,线性相关越大。
越接近1,线性相关越大。
下表给出相关系数的起码值(它与观测次数n及所给信度![]() 有关),当
有关),当![]() 大于表中相应的值,所配的直线才有意义。
大于表中相应的值,所配的直线才有意义。
| N—2 |
|
| n-2 |
|
| n-2 |
|
|
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 0.997 0.950 0.878 0.811 0.754 0.707 0.666 0.632 0.602 0.576 0.553 0.532 0.514 0.497 0.482 | 1.000 0.990 0.959 0.917 0.874 0.834 0.798 0.765 0.735 0.708 0.684 0.661 0.641 0.623 0.606 | 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | 0.468 0.456 0.444 0.433 0.423 0.413 0.404 0.396 0.388 0.381 0.374 0.367 0.361 0.355 0.349 | 0.590 0.575 0.561 0.549 0.537 0.526 0.515 0.506 0.496 0.487 0.478 0.470 0.463 0.456 0.449 | 35 40 45 50 60 70 80 90 100 125 150 200 300 400 1000 | 0.325 0.304 0.288 0.273 0.250 0.232 0.217 0.205 0.195 0.174 0.159 0.138 0.113 0.098 0.062 | 0.418 0.393 0.372 0.354 0.325 0.302 0.283 0.267 0.254 0.228 0.208 0.181 0.148 0.128 0.081 |
 注意,当观测次数n很大时 ,相关系数可用下述方法近似求得:将观测数对(xi , yi) (i=1,2,···,n)描在坐标纸上,先作一水平直线使位在直线的上下点数相等,再作一垂直线使左右点数相等,这两条直线(尽量使两直线上没有点)将平面分成四块(图16.5)设落在右上方,左上方,左下方,右下方的点数分别为n1 ,n2,n3 , n4,设
注意,当观测次数n很大时 ,相关系数可用下述方法近似求得:将观测数对(xi , yi) (i=1,2,···,n)描在坐标纸上,先作一水平直线使位在直线的上下点数相等,再作一垂直线使左右点数相等,这两条直线(尽量使两直线上没有点)将平面分成四块(图16.5)设落在右上方,左上方,左下方,右下方的点数分别为n1 ,n2,n3 , n4,设
n+=n1+n3 ![]() =n2+n4
=n2+n4
那末相关系数近似为

[剩余标准差]


称为剩余标准差,它描述回归直线的精度:对于试验范围的每个x,有95.4%的y值落在两条平行直线
![]()
之间(图16.6);有99.7%的y值落在两条平行直线
![]()
之间.
[一元回归计算步骤] 为了方便计算,将lxx,lyy ,lxy改写成

并将数据整数化.即令
![]()

经整数化后,有
![]()
![]() ,
, ![]()
![]()
![]()
![]()
于是列表计算如下:
| 序号 | | | | | | |||
| 1 2 n | | | | | | |||
| | | | | | | |||
|
| | | | | | |||
|
| | |
|
| | |||
| 记号 |
|
|
- |
- | - | |||
| 计 算 结 果 | 回归系数 常数项 回归方程 相关系数 剩余标准差 |
| |||||
|
|
|
|
|
|
|
|
|
|
[一元线性回归的方差分析] 将自变量x看作单因素,对每个xi(i=1,2,···,n)作k次重复试验得到数据yij(i=1,2,···,n; j=1,2,···,k),记录如下:
|
| yij |
|
| x1 x2 | y11 y12 ··· y1k y21 y22 ··· y2k
yn1 yn2 ··· ynk |
|
|
|
|
|
按照数对![]() 求出回归方程
求出回归方程
![]()
![]()
y的总平方和为
![]()
记作
![]()
上述右边的S回称为回归平方和,它是由于x的变化使y也随之变化而引起的;S误称为误差平方和,它是由试验误差引起的;S余称为剩余平方和,它是由其他随机因素或回归直线配得不适当而引起的.
同单因素方差分析类似,作一元线性回归方差分析表如下:
| 方差来源 | 平方和 | 自由度 | 均 方 | 统计量 | 置信限 | 统计推断 |
| 回归 剩余 误差 | S回 S余 S误 | k n n | s回
|
|
| 当 当 |
| 总平方和 | S总 | nk |
|
|
|
|
检验![]() 时,若影响不显著,则表明剩余平方和基本上是试验误差等随机因素引起的;若影响显著,则表明可能存在另外不可忽略的因素,或者x与y不是直线相关,或者x与y无关。这时求出的回归直线不能刻划x与y之间的关系,需进一步查明原因,重新配线。
时,若影响不显著,则表明剩余平方和基本上是试验误差等随机因素引起的;若影响显著,则表明可能存在另外不可忽略的因素,或者x与y不是直线相关,或者x与y无关。这时求出的回归直线不能刻划x与y之间的关系,需进一步查明原因,重新配线。
检验![]() 时,若影响显著,则表明x与y之间有线性关系;若影响不显著,则需重新配线。
时,若影响显著,则表明x与y之间有线性关系;若影响不显著,则需重新配线。
S总,S回,S余,和S误按下列公式计算(可先将数据整数化![]() ,
, ![]() :
:
S总=
S回=![]()
S余=
S误= S总![]() 回
回![]() 余
余
式中
![]()