§ 4  尺度空间与一致空间

一、  一、    尺度空间

    [尺度、距离与尺度空间]  假定D是一个集，j是一个把D´D变进R¹的变换，如果对于所有的xD，yD，zD，满足条件：

    (i)  j（x，y）³0，等号只当x=y时成立，这里j（x，y）=j（<x，y>）；

    (ii)  j（x，y）=j（y，x）；

    (iii)  j（x，y）+j（y，z）³j（x，z）.

那末称j为D的一个尺度，j（x，y）是在j这个尺度下x和y的距离，D是以j为尺度的尺度空间（距离空间）.

   如果条件（i）中不附加“等号只当x=y时成立”，其余（ii），（iii）相同，那末称j为D的一个拟尺度.

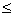    [尺度空间的拓扑]  假定j是集D的一个尺度，对一点aD和一个实数r，把{x|j（x，a）<r}（当r0时它表示空集）称为以a为球心r为半径的开球.所有开球全体所繁殖的拓扑称为D的尺度拓扑.实际上，所有开球的全体是这个拓扑的一个基.以后如果没有另外声明，凡是尺度空间都假定是以这个尺度拓扑为拓扑的拓扑空间.

   假定a是尺度空间里的一点，那末所有以a为球心，把有理数作为半径的开球的全体是a的一个邻域基.所以尺度空间一定是第一可数空间.此外也不难看到，尺度空间一定是T₂空间.

    [尺度化与尺度化定理]  假定一个拓扑空间X的承载点集有一个尺度，由这尺度得到的拓扑跟X原有的拓扑相等，那末称X可以尺度化.

   假定Φ是拓扑空间X里的一族点集的全体.如果X里每一点都有一个邻域至多只跟有限个属于Φ的点集有公共点，那末称Φ是局部有限的；特别如果任何两个属于Φ的点集的包都没有公共点，那末称Φ是绝缘的.

   定理  一个拓扑空间X可以尺度化的充分必要条件是：X为T₃空间并且X的拓扑有一个基是可数个局部有限族的和集（这里“局部有限”可以改作“绝缘”， T₃也可以改作T₄）.

    [n维欧氏空间与直角坐标法]  假定X是一个以j为尺度的尺度空间，又假定存在一个把X变上n维实数空间Rⁿ的一对一变换f，使对X里任何两点x和y，

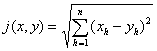
成立,这里，那末称X为n维欧几里得空间，简称n维欧氏空间，记作Eⁿ，f是Eⁿ的一个直角坐标法，称为点x的直角坐标，称为这直角坐标法下的原点.

    E ⁿ的直角坐标法存在但是不唯一.假定f和都是E ⁿ的直角坐标法，f '（O_f）=<b₁,×××,b_n>，而E ⁿ里任何一点x在f和f '下的坐标分别记作<x₁,×××,x_n>和<x₁ ',×××,x_n'>，那末由于

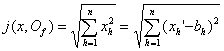
得到

这里（a_hk）是一个n´n正交矩阵.

   反过来，只要（a_hk）是任何一个n´n正交矩阵,b₁,×××, b_n是任何n个实数，那末上面这组方程就代表了一个新的直角坐标法.所以直角坐标法是无限多的，而不同的直角坐标法间的变换就是通常所谓“转轴”、“移轴”的组合.

   此外，Eⁿ的一个直角坐标法f实际上是把Eⁿ变上Rⁿ的一个拓扑变换，因此Eⁿ里的一个开球在f下的象是Rⁿ里的一族n维区间的和集，反过来，Rⁿ里一个n维区间的象源是Eⁿ里的开球的和集.

   因此在Rⁿ里可以定一个尺度，使它成为Eⁿ.这同时也就证明了n维欧氏空间的存在.

    [空间的完备化]  假定X是一个以j为尺度的尺度空间.如果<x_n|nω>是X里的一个点列，对任何正数e ，总存在一个正整数N，使

                              j（x_n, x_m）<e

对比N大的一切正整数n和m都成立，那末称<x_n|nω>是X里的柯西列.

   一个尺度空间里的任何一个收敛点列一定是柯西列，但是一个柯西列未必收敛.例如，把所有的有理数全体S看作一维实数空间R¹的子空间的话，那末S里的柯西列就可能不收敛（因为它的极限可能是无理数）.

   如果一个尺度空间X里的任何柯西列都收敛，那末称X完备.

   假定X和X'都是尺度空间，X'完备，又假定存在一个把X等尺度同胚地变进X'的变换f，并且X的象f（X）在X'里处处稠密，那末称X'为X的完备化.

   定理  任何一个尺度空间都有完备化，并且任何两个完备化等尺度同胚.

   只要把尺度空间里一个柯西列看作一个元素，适当规定两个柯西列的距离（距离等于零时，认为两个元素是相同的）不难证明所有这些元素全体就是一个完备化.

   把两个实数的差的绝对值看作这两个实数的距离，那末一维实数空间R¹就是所有的有理数全体的完备化.可以用这个办法来建立无理数的概念.

   柯西列当然可以推广成柯西网.不过由于尺度空间满足第一可数公理，用柯西网概念只能得到同样的完备化.

    [有界变换族的一致收敛拓扑]  假定A是一个集，Y是一个尺度空间，把A变进Y 的所有有界变换（把A变进一个开球的变换称为有界变换）的全体记作F.在F里规定距离如下：设fF，gF，则它们的距离

                      J（f，g）= j（f（x），g（x））

这里j表示Y里的尺度.由J所产生的F的尺度拓扑称为F的一致收敛拓扑.

   注意，F的一致收敛拓扑只用Y的尺度定义，没有牵涉到A的拓扑.

   定理 有界变换族F的一致收敛拓扑跟其他拓扑比较起来其特点是：在这拓扑下，F里任何一个点网<f_p|pQ>收敛的充分必要条件是：对所有的xA, <f_p(x)|pQ>在A里一致收敛（也就是对任何正数e ，存在一个qQ，是对所有的xA和Q里所有的p>q,

                            j（f_p(x)，f_q(x)）<e

成立）.

    F可以看作^AY的子集.因此^AY 的点点收敛拓扑在F里有诱导拓扑，不妨称为F的点点收敛拓扑，因为同样是用“点点收敛”当收敛的.比较起来，一致收敛拓扑比点点收敛拓扑细.因为在一致收敛拓扑下，对每一点fF，所有的集{g|对所有的xA, j（g（x），f（x））<e }（e 是一个任意正数）构成一个邻域基.而在点点收敛拓扑下，对每个fF，所有的集{g|存在有限个xA使j（g(x)，f(x)）<e }构成一个邻域基.后一个邻域基里的每一个集显然都掩盖前一个邻域基里的一个集，但是倒过来说不行.