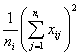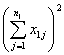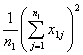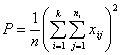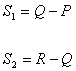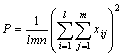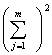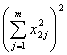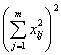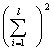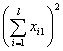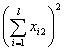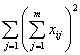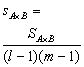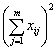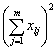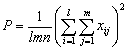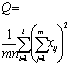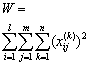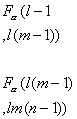三、方差分析
方差分析是分析试验(或观测)数据的一种方法,它所要解决的基本问题是通过数据的分析,弄清与研究对象有关的各个因素以及各个因素之间的交互作用对该对象的影响。它所研究的对象都假定遵从正态分布。
[单因素方差分析] 考虑一个因素A的不同水平对所考察的对象的影响。对A的k个不同水平Ai(其分布![]() 进行试验,得试验数据
进行试验,得试验数据![]()
![]() ;
;![]() nk)假定
nk)假定![]() (尽管数值未知),检验各Ai的试验结果的平均值有无显著差异。其检验步骤如下:
(尽管数值未知),检验各Ai的试验结果的平均值有无显著差异。其检验步骤如下:
(1)假设
(2)选取统计量并明确其分布

式中
![]()
![]()
(3)给出显著性水平![]()
(4)由F分布表(自由度为(k-1,n-k))可以查出置信限![]() ,它满足
,它满足
![]()
(5)列表计算统计量。
| 分级 | 试验数据xij | ni |
|
|
|
| |
| A1 A2
Ak |
| n1 n2 nk |
|
|
|
| |
|
|
|
|
|
|
|
| |
| 记号 |
| |
| ||||
|
|
|
|
|
|
|
|
|
(6) 单因素方差分析表
| 方差 来源 | 平方和 | 自由度 | 均 方 | 统计量 | 置信限 | 统计推断 |
| 组间 组内 |
| k n |
|
|
| 当 当 |
| 总和 |
| n |
|
|
|
|
说明:1° 若![]() 的数值较大,取
的数值较大,取![]() 为某常数,则用
为某常数,则用![]() 代替
代替![]() 进行上述计算,其分析结果不变。2° 组间方差S1反映了因素A的不同水平引起的系统误差,而组内方差S2则是随机因素引起的组内差异。如果不同因素Ai所起的作用差不多,组间方差与组内方差之比就较小,则可认为
进行上述计算,其分析结果不变。2° 组间方差S1反映了因素A的不同水平引起的系统误差,而组内方差S2则是随机因素引起的组内差异。如果不同因素Ai所起的作用差不多,组间方差与组内方差之比就较小,则可认为![]() ;如果不同因素Ai所起的作用显著不同,组间方差与组内方差之比就较大,就不能认为
;如果不同因素Ai所起的作用显著不同,组间方差与组内方差之比就较大,就不能认为![]() 。
。
[双因素方差分析] 考虑两个因素A和B的影响。A分成l个等级A1 , A2 , ··· ,Al。B分成m个等级B1 , B2 , ···,Bm 在双因素Ai![]() j 条件下(即每次试验都要让Ai与Bj作lm种配合)作n次试验,得lmn个数据
j 条件下(即每次试验都要让Ai与Bj作lm种配合)作n次试验,得lmn个数据![]() 。假定
。假定![]() 的分布
的分布![]() ,检验A的作用或B的作用或
,检验A的作用或B的作用或![]() 的作用分别对试验结果有无显著影响。其检验步骤如下:
的作用分别对试验结果有无显著影响。其检验步骤如下:
(1)假设H0 :对应的作用(A或B或![]() )对试验结果无显著影响。
)对试验结果无显著影响。
(2)选取统计量并明确其分布

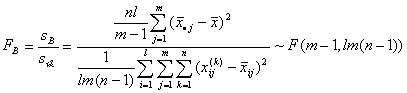
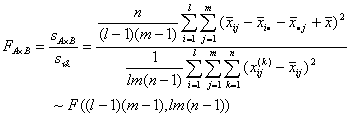
式中FA , FB 及![]() 分别表示因素A的作用,B的作用及因素A与B的交互作用,且
分别表示因素A的作用,B的作用及因素A与B的交互作用,且
![]() ,
,![]()
![]()
![]()
(3) 给出信度![]() 。
。
(4) 查出置信限![]() 。当自由度为
。当自由度为![]() ,则
,则![]() 满足
满足
![]()
(5) 列表计算统计量(表1和表2)。
表1
| A | B | 试验结果 |
|
|
| |
| A1 | B1 B2
Bm |
| | |
| |
|
|
| | | | | |
| Al | B1 B2
Bm |
| | |
| |
|
|
| |
|
| |
| 记号 |
|
|
| ||
表2
|
| B1 B2 ... Bm |
|
|
| A1 A2 Al | x11 x12 ... x1m x21 x22 ... x2m xl1 xl2 ... xlm |
|
|
| | | |
|
|
|
|
|
|
(6) 双因素方差分析表
| 方差 来源 | 平方和 | 自由度 | 均 方 | 统 计 量 | 置 信 限 | 统计推断 |
| A的 作用 B的 作用 | SA=Q SB=R | l m |
|
|
| 当
|
|
的作用 随机作用 | SA T–Q S误=W | (l lm(n |
|
|
| 当
|
| 总平 方和 | S | lmn |
|
|
|
|
当A,B两个因素的交互作用不显著时,SA![]() B与S误混合在一起,这时若在
B与S误混合在一起,这时若在![]() 条件下只作一次试验(即n=1),测得试验数据为xi j,记
条件下只作一次试验(即n=1),测得试验数据为xi j,记
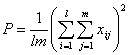

则
![]()
这时,因素A及因素B的统计量与分布分别为
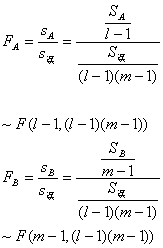
计算过程和方差分析同前。
[系统分组的方差分析] 作调查时常采用按系统分组的方法。例如到某县调查时,选几个公社,每个公社又分别选几个大队,每个大队又选几个生产队。这种方法称为系统分组。
系统分组的方差分析与多因素方差分析是不同的。譬如双因素方差分析中,因素A , B是平行的,而在系统分组的方差分析中,A , B不是平行的,它是先按因素A分组为A1 , A2, ··· , Al ,然后在每一组Ai中再按因素B分组为Bi1 , Bi2 ,···, Bim。不过,分析的方法是类似的。
设在因素Ai和因素Bij的条件下作n次试验,试验数据为![]() ,其检验步骤如下:
,其检验步骤如下:
(1) 假设H0:在![]() 条件下,因素A(或B)影响不显著。
条件下,因素A(或B)影响不显著。
(2) 选取统计量

式中FAB和FB分别表示因素A和因素B的影响的显著性,而且
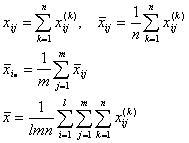
(3) 给出信度![]() 。
。
( 4 ) 查出置信限![]() 。当自由度为
。当自由度为 时,
时, 满足
满足
![]()
(5) 列表计算统计量
|
|
| 试验结果xij(k) |
|
|
|
|
| |
| A1 | B11 B12
|
| x11 x12 x1m |
|
| |
| |
|
|
|
| | | | | | |
| Al | Bl1 Bl2
Blm |
| x11 x12 x1m |
|
|
|
| |
|
|
|
|
|
|
| |||
| 记号 |
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
(6) 系统分组方差分析表
| 方差来源 | 平方和 | 自由度 | 均 方 | 统计量 | 置信限 | 统计推断 |
| A的作用 B的作用 随机作用 | SA=Q-P SB=T-Q S误=W-T | l-1 l(m-1) lm(n-1) |
|
|
| 当 当 |
| 总平方和 |
| lmn |
|
|
|
|