三、巴拿赫空间
[赋范线性空间] 设V为一个线性空间，对于V中每个元素α，有一个实数
与之对应，且具有下列性质：
(i) 
，当且仅当
时
；
(ii) 
，特别
；
(iii) 
；
则称V为赋范线性空间. 
称为α的范数或模.
对于赋范线性空间V，
则V成为一个尺度空间. 以后讲到赋范线性空间，总认为它是一个尺度空间，并且用（1）式表示它的距离.
[巴拿赫空间的定义与例子] 完备的赋范线性空间称为巴拿赫空间.
例1 
是巴拿赫空间.
例2 设在
内所定义的一切连续函数的全体记为C，令
，
属于C，c是任一实数，定义
易知C是一个线性空间，对于C中的
，定义
则C为一赋范线性空间，这种空间称为空间
.
设
，则由
可得函数序列
一致收敛于
.
可以证明，空间
是完备的，所以是巴拿赫空间.
例3 例3 设有界实数列
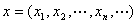
的全体记为M.设
与
是两个有界数列，a是任一实数. 定义和，数乘与范数如下：
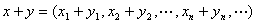
那末M成为一个赋范线性空间,称为收敛序列空间，简称为空间M. 并可证明空间M是完备的，所以是巴拿赫空间.
[紧致性] 设A为尺度空间E中一个非空集，或者A的任一无限子集
至少有一极限点，则称A是一个紧致集.
任一紧致集必为有界.
设
是定义在区间
上的一个函数族，若对任一
，恒有
，当
，且
时，不等式
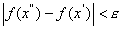
对A中任意函数
成立，则称函数族A在
上等度连续.
阿尔采拉—阿斯可里定理 设
是定义在
上的连续函数族，
若
(i) 存在一个常数M，使此族中的函数都满足
；
(ii) A在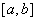
上等度连续；
则A中存在着在
上一致收敛的函数序列.
设A是空间C中的一个元素，则A为紧致的充分必要条件是：A中一切函数为有界且为等度连续.
[线性泛函及其性质] 考虑巴拿赫空间V上的泛函数v，对于V中任一点x，有一实函数
与它对应，若
(i) v是可加的，齐次的，即对V中任两点x和y与任两实数a，b，恒有
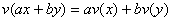
(ii) v是连续的，即当
时，
，则称
为V上的线性泛函.
线性泛函有以下性质：
1o可加齐次泛函
连续的充分必要条件是：有常数
，使
（2）
2o设
是线性泛函，则由满足（2）的一切M构成数集的下确界称为
的模或范数，记作
；且有
3o若对巴拿赫空间V上一个线性泛函序列{
}，使
在V上处处存在，则有常数
，使得
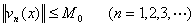
这称为一致有界原理或共鸣定理.