2. 双曲型方程的黎曼方法
考虑拉普拉斯双曲型方程
![]()
[古沙问题的特征线法] 古沙问题是
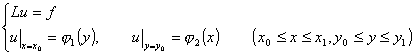
设a(x,y),b(x,y),c(x,y),f(x,y)为连续函数;![]() 连续可微且
连续可微且![]() ,令
,令
![]()
则古沙问题化为下面积分方程组的求解问题
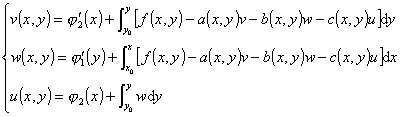
|
图14.6 |
它可用逐次逼近法求解,显然x=x0,y=y0为拉普拉斯双曲型方程的特征线,所以此法也称为特征线法.
[广义柯西问题的黎曼方法] 广义柯西问题是
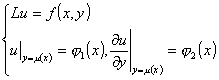
设a(x,y),b(x,y),c(x,y),![]() 1(x)及(x)为连续可微函数,且'(x)≠0,而f(x,y)及
1(x)及(x)为连续可微函数,且'(x)≠0,而f(x,y)及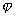 2(x)为连续函数.
2(x)为连续函数.
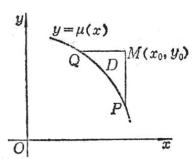
设M(x0,y0)不是y=(x)上的点,过点M作特征线x=x0,y=y0交y=(x)于P及Q,记曲边三角形PMQ为D(图14.6),在D上用格林公式(本节,四)得
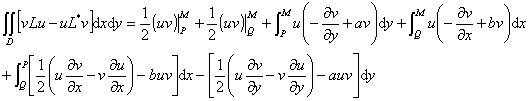
设v(x,y;x0,y0)为下面古沙问题的解:
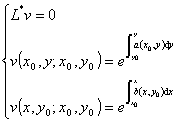
那末广义柯西问题解的黎曼公式为
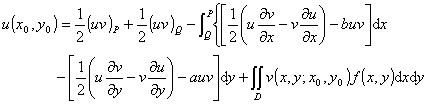
式中v(x,y;x0,y0)称为黎曼函数,这个方法称为黎曼方法.
一般可用特征线法求黎曼函数.但对常系数偏微分方程
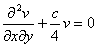 (c为常数)
(c为常数)
也可用下法求黎曼函数.设v=v(z),![]() ,则方程化为贝塞耳方程
,则方程化为贝塞耳方程
![]()
黎曼函数就是满足此贝塞耳方程及条件v(0)=1的零阶贝塞耳函数,
![]()
对常系数的拉普拉斯双曲型方程通过变换可化为
![]()
的形式,它的黎曼函数就是上式.