§2  场论初步

一、  一、场论的基本概念及梯度、散度与旋度

[标量场]  空间区域D的每点M(x,y,z)对应一个数量值(x,y,z)，它在此空间区域D上就构成一个标量场，用点M(x,y,z)的标函数(x，y，z)表示.若M的位置用矢径r确定，则标量可以看作变矢r的函数＝(r).

例如温度场u(x,y,z),密度场,电位场e(x,y,z)都是标量场.

    [矢量场]  空间区域D的每点M(x，y，z)对应一个矢量值r(x，y，z)，它在此空间区域D上就构成一个矢量场，用点M(x，y，z)的矢量函数r(x，y，z)表示.若M的位置用矢径r确定，则矢量r可以看作变矢r的矢函数r(r)：

R(r)＝X(x，y，z)i＋Y(x，y，z)j＋Z(x，y，z)k

    例如流速场 (x，y，z)，电场E(x，y，z)，磁场H(x，y，z)都是矢量场.

与标量场的情况一样，矢量场概念与矢函数概念，实质上是一样的.沿用这些术语(标量场、矢量场)是为了保留它们的自身起源与物理意义.

[梯度]

grad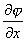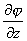＝(，，)==i＋j＋k

式中=i＋j＋k称为哈密顿算子,也称为耐普拉算子.grad有的书刊中记作del.

    grad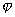的方向与过点(x，y，z)的等量面＝C的法线方向N重合，并指向增加的一方，是函数变化率最大的方向，它的长度等于.

梯度具有性质：

grad(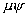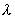＋)＝ grad＋grad    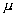(、为常数)

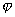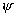            grad()＝ grad＋ grad

            gradF()＝

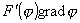
[方向导数]

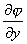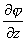＝l·grad＝cos＋cos＋cos

式中l＝(cos,cos,cos)为方向l的单位矢量,,,为其方向角.

方向导数为在方向l上的变化律，它等于梯度在方向l上的投影.

[散度]

divr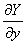＝＋＋=·r=div(X , Y , Z)

式中为哈密顿算子.

    散度具有性质：

    div(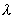a＋b)＝ diva＋divb   (、为常数)

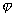    div(a)＝div a＋a grad

    div(a×b)＝b·rot a－a·rotb

[旋度]

       rotr＝()i＋()j＋()k=×r=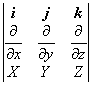

式中为哈密顿算子，旋度也称涡度，rot r有的书刊中记作curl r.

旋度具有性质：

rot(a＋b)＝ rot a＋rot b   (、为常数)

rot(a)＝rot a＋a×grad

rot(a×b)＝(b·)a－(a·)b＋(div b)a－(div a)b

[梯度、散度、旋度混合运算] 运算grad作用到一个标量场产生矢量场grad，运算div作用到一个矢量场 r产生标量场div r，运算rot作用到一个矢量场r产生新的矢量场

rot r.这三种运算的混合运算公式如下：

div rot r＝０

rot grad＝０

div grad＝ ＋＋=

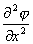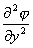grad div r＝(r)

rot rot r＝×(×r)

div grad(+)= div grad+div grad    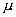(、为常数)

div grad()=div grad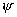＋div grad ＋２grad·grad

grad div r－rot rot r＝r

式中  为哈密顿算子，＝·＝^２为拉普拉斯算子.

    [势量场(守恒场)]  若矢量场r(x，y，z)是某一标函数(x，y，z)的梯度，即

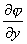r＝grad 或 X＝，Y＝，Z＝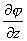

则r称为势量场，标函数称为r的势函数.

矢量场r为势量场的充分必要条件是：rot r＝０，或

 =,=,=

势函数计算公式

(x，y，z)＝(x₀，y₀，z₀)＋＋

＋

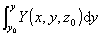
[无散场(管形场)]  若矢量场r的散度为零，即div r＝0，则r称为无散场.这时必存在一个无散场T，使r＝rot T，对任意点M有

T＝

式中r为dV到M的距离，积分是对整个空间进行的.

     [无旋场]  若矢量场r的旋度为零，即rot r＝0，则r称为无旋场.势量场总是一个无旋场，这时必存在一个标函数，使r＝grad，而对任意点M有

＝－

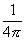
式中r为dV到M的距离，积分是对整个空间进行的.