三、对偶空间与对偶映射

    [数量积与对偶空间]  设V和是两个实（复）线性空间. 若对任意一对矢量确定了一个数量，并满足下列条件：

(i)                                 (i)     

(ii) 对一个固定的和一切,若则；反之，对一个固定的和一切,若则.则称函数为数量积.

若，则称是正交的. (ii)表明，一个空间中一个矢量与另一个空间中一切矢量正交，只当它是零矢量时才成立.

定义了数量积的两个线性空间称为对偶空间.

对偶空间的维数相等.

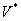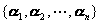[对偶基底]  若V和的两个基底和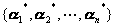满足关系式：

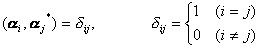
则称它们为对偶基底.

    V和是对偶空间，则对于V的一个已知基底，恰有一个对偶基底.

[正交补空间]  设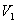是V的一个子空间，则空间V中与的一切矢量都正交的矢量组成的集合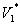是V的一个子空间，称为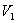的正交补空间，记作.

正交补空间有以下性质：

1^o空间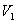和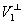的维数之和等于空间V的维数，即

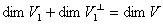
2^o

3^o若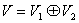，则；而且和是一对对偶空间，和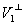也是一对对偶空间.

    [共轭空间]  设V是域F上的线性空间，若对，在F上有唯一的一个数与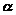对应，则称这个对应关系为定义在V上的一个函数.

    函数

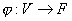
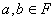若对任二矢量与任意，都有

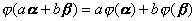
则称为线性函数，又称为线性泛函. 令，则有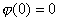，因此又称线性函数为线性齐次函数或线性型.

    V中线性函数的集的两个函数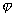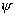，的和与数乘按通常的方式定义如下：

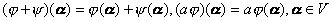
则构成一个线性空间，称为V的共轭空间，的零矢量是一个恒等于零的函数.

    可以证明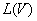和V是一对对偶空间，若{}是V的一组基底，则由下列方程定义的函数为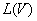的一个基底：

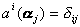
因而{}又是{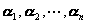}的共轭基底.

[对偶映射]  设V，与W，是两对对偶空间；若两个线性映射：

                                         与

对于一切与一切，都有

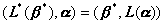
则称L，为对偶映射.

对偶映射有以下性质：

1^O对一个已知的线性映射，恰有一个对偶映射.

2^O对偶映射L和的秩相等.

3^O一个矢量包含在象空间中的充分必要条件是：与核中的一切矢量正交.